สูตรการหาพื้นที่และปริมาตรต่างๆ

1. สูตรการหาพื้นที่สี่เหลี่ยมจัตุรัส = ด้าน x ด้าน หรือ 1/2 x ผลคูณของเส้นทแยงมุม

2. สูตรการหาพื้นที่สี่เหลี่ยมผืนผ้า = กว้าง x ยาว

3. สูตรการหาพื้นที่สามเหลี่ยม = 1/2 x ฐาน x สูง

4. สูตรการหาพื้นที่สี่เหลี่ยมขนมเปียกปูน = ฐาน x สูง หรือ 1/2 x ผลคูณของเส้นทแยงมุม

5. สูตรการหาพื้นที่สี่เหลี่ยมด้านขนาน = ฐาน x สูง

6. สูตรการหาพื้นที่สี่เหลี่ยมรูปว่าว = 1/2 x ผลคูณของเส้นทแยงมุม

7. สูตรการหาพื้นที่สี่เหลี่ยมด้านไม่เท่า = 1/2 x เส้นทแยงมุม x ผลบวกของเส้นกิ่ง

8. สูตรการหาพื้นที่วงกลม = พาย x รัศมี²

9. สูตรการหาปริมาตรทรงลูกบาศก์ = ด้าน³

10. สูตรการหาปริมาตรทรงสี่เหลี่ยมมุมฉาก = กว้าง x ยาว x สูง

11. สูตรการหาปริมาตรทรงกลม = 4/3 x พาย x รัศมี³

12. สูตรการหาปริมาตรทรงกระบอก = พาย x รัศมี² x สูง

13. สูตรการหาปริมาตรทรงกรวย = 1/3 x พาย x รัศมี² x สูง

14. สูตรการหาปริมาตรปริซึม = พื้นที่ฐาน x สูง

อ้างอิง http://www.trueplookpanya.com  21/ 08 / 2556

จำนวนเต็มแบ่งออกเป็น 3 ชนิด
จำนวนเต็มลบ คือ จำนวนที่มีค่าน้อยกว่า ศูนย์ มีตำแหน่งอยู่ทางด้านซ้ายมือของศูนย์เมื่ออยู่บนเส้นจำนวน และ จะมีค่าลดลงเรื่อย ๆ โดยไม่สามารถจะบอกได้ว่าจำนวนใดจะมีค่าน้อยที่สุด แต่เราสามารถรู้ได้ว่าจำนวนเต็มลบที่มีค่ามากที่สุด คือ -1 เราพอจะสรุปลักษณะที่สำคัญของจำนวนเต็มลบได้ดังนี้ 
1. จำนวนเต็มลบเป็นจำนวนที่มีค่าน้อยกว่าศูนย์ หรือถ้ามองบนเส้นจำนวน ก็คือ เป็นจำนวนที่อยู่ทางซ้ายมือของศูนย์ 
2. จำนวนเต็มลบที่มีน้อยที่สุดไม่สามารถหาได้ แต่ จำนวนเต็มลบที่มีค่ามากที่สุด คือ -1
3. ตัวเลขที่ตามหลังเครื่องหมายลบ ถ้ายิ่งมีค่ามากขึ้นจำนวนเต็มลบนั้นจะมีค่าน้อยลง 
กล่าวคือ ...-5 < -4 < -3 < -2 < -1 

ศูนย์ ( ใช้สัญลักษณ์ "0" ) เป็นจำนวนเต็มอีกชนิดหนึ่ง ที่เราไม่ถือว่าเป็นจำนวนนับ จากหลักฐานที่ค้นพบทำให้เราทราบว่ามนุษย์รู้จักใช้สัญลักษณ ์ "0" ในราวปี ค.ศ. 800 โดยที่ "0" แทนปริมาณของการไม่มีของหรือของที่ต้องการกล่าวถึง แต่ก็ไม่ใช่ว่า 0 จะไม่มีความหมายถึงการไม่มีเสมอไป ตัวอย่างเช่น ระดับผลการเรียนทางด้านความรู้ โดยนักเรียนที่มีระดับผลการเรียนเป็น 0 ไม่ได้หมายความว่านักเรียนคนนั้นไม่มีความรู้ เพียงแต่ ว่ามีความรู้ในระดับหนึ่งเท่านั้น
จำนวนเต็มบวก หรือ จำนวนนับ คือ จำนวนเต็มที่มีค่ามากกว่า 0 ไปเรื่อย ๆ โดยที่ไม่สามารถระบุได้ว่าจำนวนนับตัวสุดท้ายเป็นอะไร จำนวนนับเริ่มต้นที่ 1 , 2 , 3, ... ซึ่งเราทราบแล้วว่า จำนวนนับที่น้อยที่สุด คือ 1จำนวนนับที่มากที่สุดหาไม่ได้ คุณสมบัติของศูนย์และหนึ่ง
อ้างอิง http://eduvc.oas.psu.ac.th/~user192/content1.html 21/08/2556

รูป เรขาคณิต หมายถึง รูปต่างๆ ทางเรขาคณิต เช่น
รูปสามเหลี่ยม มีด้าน 3 ด้าน มีมุม 3 มุม

รูปสี่เหลี่ยม มีด้าน 4 ด้าน มีมุม 4 มุม

รูปห้าเหลี่ยม มีด้าน 5 ด้าน มีมุม 5 มุม

รูปหกเหลี่ยม มีด้าน 6 ด้าน มีมุม 6 มุม

รูปแปดเหลี่ยม มีด้าน 8 ด้าน มีมุม 8 มุม

รูปวงกลม มีเส้นโค้งเป็นวงกลม และห่างจากจุดศูนย์กลางเป็นระยะทางเท่ากัน

รูปวงรี มีเส้นเส้นโค้งเป็นวงรี โดยห่างจากจุดศูนย์กลางไม่เท่ากัน



รูปทรง เรขาคณิตรูปทรงเรขาคณิต หมายถึง รูปที่มีส่วนที่เป็นพื้นผิว ส่วนสูง และส่วนลึก หรือหนา

รูปทรงกลม


รูปทรงสี่เหลี่ยมมุมฉาก


รูปทรงกระบอก


รูปเรขาคณิตสามมิติ

ระดับชั้นมัธยมต้นนี้ นักเรียนควรมีพื้นฐานเกี่ยวกับ พื้นที่ผิวและปริมาตรที่ควรทราบ ดังนี้

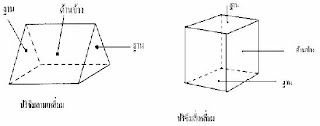
ปริซึม

ปริซึม เป็นรูปเรขาคณิตสามมิติที่มีหน้าตัด(ฐาน) ทั้งสองข้างเป็นรูปหลายเหลี่ยมที่เท่ากันทุกประการหน้าตัด (ฐาน) ทั้งสองอยู่ในระนาบที่ขนานกัน มีหน้าข้างเป็นรูปสี่เหลี่ยมมุมฉาก การเรียกชื่อปริซึมจะเรียกตามรูปหน้าตัดของปริซึมส่วนต่างๆของปริซึมมีชื่อเรียก ดังนี้

ทรงกระบอก

ทรงกระบอก เป็นรูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยู่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ ด้านข้างเป็นผิวเรียบโค้งส่วนต่างๆของทรงกระบอก
ข้อแตกต่างของปริซึมกับทรงกระบอก คือ
- ฐาน ปริซึมเป็นรูปหลายเหลี่ยมทรงกระบอกเป็นวงกลม- ด้านข้าง ปริซึมเป็นรูปสี่เหลี่ยมผืนผ้าทรงกระบอกเป็นผิวเรียบโค้ง
พีระมิด

พีระมิด เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยุ่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น การเรียกชื่อพีระมิดจะเรียกตามรูปฐานของพีระมิด
ส่วนต่างๆของพีระมิด



กรวย

กรวย เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรงดด้านข้างเป็นผิวโค้งเรียบระมิ
ส่วนต่างๆของกรวย
ข้อแตกต่างของพีระมิดกับกรวย คือ- ฐาน พีระมิดฐานรูปหลายเหลี่ยมกรวยฐานรูปวงกลม
- ด้านข้าง พีระมิดเป็นรูปสามเหลี่ยมผืนผ้า
กรวยเป็นผิวเรียบโค้ง

ทรงกลม

ทรงกลม เป็น รูปเรขาคณิตสามมิติที่มีด้านข้างเป็นผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดคงที่จุดหนึ่งเป็นระยะเท่ากัน เรียกจุดคงที่ว่า จุดศูนย์กลางของทรงกลม
เรียกระยะที่เท่ากันว่า รัศมีของทรงกลม
ส่วนต่างๆของทรงกลม

                                                                    

รูป เรขาคณิต หมายถึง รูปต่างๆ ทางเรขาคณิต เช่น
รูปสามเหลี่ยม มีด้าน 3 ด้าน มีมุม 3 มุม

รูปสี่เหลี่ยม มีด้าน 4 ด้าน มีมุม 4 มุม

รูปห้าเหลี่ยม มีด้าน 5 ด้าน มีมุม 5 มุม

รูปหกเหลี่ยม มีด้าน 6 ด้าน มีมุม 6 มุม

รูปแปดเหลี่ยม มีด้าน 8 ด้าน มีมุม 8 มุม

รูปวงกลม มีเส้นโค้งเป็นวงกลม และห่างจากจุดศูนย์กลางเป็นระยะทางเท่ากัน

รูปวงรี มีเส้นเส้นโค้งเป็นวงรี โดยห่างจากจุดศูนย์กลางไม่เท่ากัน



รูปทรง เรขาคณิตรูปทรงเรขาคณิต หมายถึง รูปที่มีส่วนที่เป็นพื้นผิว ส่วนสูง และส่วนลึก หรือหนา

รูปทรงกลม


รูปทรงสี่เหลี่ยมมุมฉาก


รูปทรงกระบอก


รูปเรขาคณิตสามมิติ

ระดับชั้นมัธยมต้นนี้ นักเรียนควรมีพื้นฐานเกี่ยวกับ พื้นที่ผิวและปริมาตรที่ควรทราบ ดังนี้

ปริซึม

ปริซึม เป็นรูปเรขาคณิตสามมิติที่มีหน้าตัด(ฐาน) ทั้งสองข้างเป็นรูปหลายเหลี่ยมที่เท่ากันทุกประการหน้าตัด (ฐาน) ทั้งสองอยู่ในระนาบที่ขนานกัน มีหน้าข้างเป็นรูปสี่เหลี่ยมมุมฉาก การเรียกชื่อปริซึมจะเรียกตามรูปหน้าตัดของปริซึมส่วนต่างๆของปริซึมมีชื่อเรียก ดังนี้

ทรงกระบอก

ทรงกระบอก เป็นรูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยู่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ ด้านข้างเป็นผิวเรียบโค้งส่วนต่างๆของทรงกระบอก
ข้อแตกต่างของปริซึมกับทรงกระบอก คือ
- ฐาน ปริซึมเป็นรูปหลายเหลี่ยมทรงกระบอกเป็นวงกลม- ด้านข้าง ปริซึมเป็นรูปสี่เหลี่ยมผืนผ้าทรงกระบอกเป็นผิวเรียบโค้ง
พีระมิด

พีระมิด เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยุ่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น การเรียกชื่อพีระมิดจะเรียกตามรูปฐานของพีระมิด
ส่วนต่างๆของพีระมิด



กรวย

กรวย เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรงดด้านข้างเป็นผิวโค้งเรียบระมิ
ส่วนต่างๆของกรวย
ข้อแตกต่างของพีระมิดกับกรวย คือ- ฐาน พีระมิดฐานรูปหลายเหลี่ยมกรวยฐานรูปวงกลม
- ด้านข้าง พีระมิดเป็นรูปสามเหลี่ยมผืนผ้า
กรวยเป็นผิวเรียบโค้ง

ทรงกลม

ทรงกลม เป็น รูปเรขาคณิตสามมิติที่มีด้านข้างเป็นผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดคงที่จุดหนึ่งเป็นระยะเท่ากัน เรียกจุดคงที่ว่า จุดศูนย์กลางของทรงกลม
เรียกระยะที่เท่ากันว่า รัศมีของทรงกลม
ส่วนต่างๆของทรงกลม


อ้างอิง http://math-tiger.blogspot.com 30/08/2556

การแยกตัวประกอบ

 ตัวประกอบ หมายถึง จำนวนนับที่หารจำนวนนับที่เรากำหนดให้ได้ลงตัว เช่น a จะเป็นตัวประกอบของ b ก็ต่อเมื่อ b หารด้วย a ลงตัว หรือกล่าวอีกนัยหนึ่งก็คือ a หาร b ลงตัว
                 ตัวอย่าง
                 30 หารด้วย 6 ลงตัว แสดงว่า 6 เป็นตัวประกอบของ 30 ในขณะที่ 30 หารด้วย 4 ไม่ลงตัว แสดงว่า 4 ไม่เป็นตัวประกอบของ 30 เป็นต้น
                 หรือ
                 จำนวนที่หาร 18 ลงตัวประกอบด้วย 1 , 2 , 3 , 6 , 9 , 18 แสดงว่า 1 , 2 , 3 , 6 , 9 , 18 เป็นตัวประกอบของ 18
                จำนวนเฉพาะ หมายถึง จำนวนที่มีตัวประกอบเพียง 2 ตัว คือ 1 กับตัวของมันเอง
                การหาตัวประกอบของจำนวนนับใด ๆ จะพบว่า บางจำนวนที่ตัวประกอบเพียง 1 ตัว บางจำนวนมีตัวประกอบ 2 ตัว ในขณะที่บางตัวมีตัวประกอบมากกว่า 2 ตัว
                1 มีตัวประกอบ 1 ตัว คือ 1
                6 มีตัวประกอบ 4 คือ 1 , 2 , 3 , 6
                2 มีตัวประกอบ 2 คือ 1 , 2 หรืออีกนัยหนึ่งว่า 2 มีตัวประกอบ 2 คือ 1 กับ ตัวของมันเอง
                3 มีตัวประกอบ 2 คือ 1 , 3 หรืออีกนัยหนึ่งว่า 3 มีตัวประกอบ 2 คือ 1 กับ ตัวของมันเอง
                จากตัวอย่างด้านบน เราพบว่า 1 มีตัวประกอบ 1 ตัว 6 มีตัวประกอบ 4 ตัว ในขณะที่ 2 และ 3 มีตัวประกอบ 2 ตัว คือ 1 กับ ตัวของมันเอง เราเรียกจำนวนที่มีตัวประกอบเพียง 2 ตัวนี้ว่า จำนวนเฉพาะ
                ตัวประกอบเฉพาะ ตัวประกอบของจำนวนนับใดที่เป็นจำนวนเฉพาะ
                การหาตัวประกอบเฉพาะของจำนวนนับใด ๆ นั้น เราจะต้องหาตัวประกอบทั้งหมดของจำนวนนับนั้น ๆก่อน จากนั้นจึงค่อยพิจารณา ตัวประกอบเหล่านั้นว่า มีจำนวนใดเป็นจำนวนเฉพาะบ้าง ซึ่งจำนวนเฉพาะเหล่านั้นเราเรีนกว่า ตัวประกอบเฉพาะ
                ตัวอย่าง
                ตัวประกอบของ 12 ประกอบ 1 , 2 , 3 , 4 , 6 , 12
                ตัวประกอบเฉพาะของ 12 ประกอบด้วย 2 , 3
               ทั้งนี้เพราะว่า 2 , 3 เป็นตัวประกอบของ 12 และเป็นจำนวนเฉพาะด้วย

 การแยกตัวประกอบ หมายถึง การเขียนในรูปการคูณของตัวประกอบเฉพาะของจำนวนนับนั้น ๆ
                ตัวอย่าง
                12 สามารถแยกตัวประกอบได้เป็น 2 x 2 x 3
                จากตัวอย่างจะพบว่า 2 และ 3 เป็นตัวประกอบเฉพาะของ 12 ซึ่งอาจมีการคูณซ้ำกันหลายครั้งก็ได้ และการคูณซ้ำกันหลายครั้ง สามารถเขียนในรูปของเลขยกกำลังได้ กล่าวคื อเราจะแยกตัวประกอบของ 12 เป็น x 3 แทน 2 x 2 x 3 ก็ได้ ( อ่านว่า 2 ยกกำลัง 2 )
                ตัวอย่างเพิ่มเติม
                75 สามารถแยกตัวประกอบได้เป็น 5 x 5 x 3 หรือ x 3
                100 สามารถแยกตัวประกอบได้เป็น 5 x 5 x 2 x 2 หรือ x

                การแยกตัวประกอบสามารถกระทำได้ดังนี้
                วิธีที่ 1 วิธีเขียนในรูปกระจายของผลคูณของตัวประกอบ
                การแยกตัวประกอบโดยวิธีนี้ เป็นการนำจำนวนนับที่กำหนดมาเขยนในรูปผลคูณของตัวประกอบทีละ 2 จำนวน โดยเขียนไปเรื่อย ๆ จนกระทั่งกลายเป็นผลคูณของตัวประกอบเฉพาะ
                ตัวอย่าง จงแยกตัวประกอบของ 80
                               80 = 8 x 10
                                    = 2 x 4 x 2 x 5
                                    = 2 x 2 x 2 x 2 x 5
                       ดังนั้น 80 = 2 x 2 x 2 x 2 x 5                                  
                       หรือ  80 = x 5
                วิธีที่ 2 วิธีตั้งหาร
                การแยกตัวประกอบโดยวิธีตั้งหาร ใช้วิธีหารสั้น ซึ่งมีขั้นตอนง่าย ๆดังนี้
                1) หารจำนวนนับที่กำหนดให้ด้วยตัวประกอบเเฉพาะของมัน
                2) หารผลหารที่ได้จากข้อ 1 ด้วยตัวประกอบเฉพาะ
                3) ดำเนินการเช่นเดียวกับข้อ 2 จนกระทั่งผลหารสุดท้ายมีค่าเท่ากับ 1
                4) นำตัวหารทั้งหมดคูณกัน จะกลายเป็นการแยกตัวประกอบของจำนวนในข้อ 1
                ตัวอย่าง จงแยกตัวประกอบของ 80
                                       2 )80      
                                       2 )40           
                                       2 )20           
                                       2 )10           
                                       5 ) 5           
                                            1
                       ดังนั้น 80 = 2 x 2 x 2 x 2 x 5
                       หรือ  80 = x 5

 ตัวหารร่วมหรือตัวประกอบร่วม หมายถึง จำนวนที่สามารถหารจำนวนนับที่กำหนดให้ตั้งแต่ 2 จำนวนลงตัว
                ขั้นตอนในการหาตัวหารร่วมจะต้องเริ่มจาก
                1) หาตัวประกอบของจำนวนที่กำหนดให้
                2) พิจารณาตัวว่าตัวประกอบใข้อ 1 ซ้ำกันหรือไม่
                3) นำตัวประกอบที่ซ้ำกันเป็นตัวหารร่วม
                ตัวอย่าง จงหาตัวหารร่วมของ 12 , 18
                         ตัวประกอบของ 12 คือ 1 , 2 , 3 , 4 ,6 , 12
                         ตัวประกอบของ 18 คือ 1 , 2 , 3 , 6 , 9 ,18
                         ดังนั้น ตัวประกอบร่วมของ 12 และ 18 คือ 1 , 2 , 3 , 6

ห.ร.ม. บางทีเรียกว่า หารร่วมมาก หมายถึง ตัวหารร่วมที่มีค่ามากที่สุด                 ห.ร.ม. จะเกิดขึ้นเมื่อมีจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป                 การหาร ห.ร.ม. สามารถหาได้หลายวิธี ดังนี้                 วิธีที่ 1 วิธีหาตัวประกอบ มีขั้นตอนดังนี้                 1) หาตัวประกอบของจำนวนนับที่กำหนดให้                2) หาตัวประกอบร่วม (ตัวหารร่วม) ของจำนวนนับในข้อ 1                 3) นำตัวหารร่วมที่มีค่ามากที่สุดในข้อ 2 เป็น ห.ร.ม.                  ตัวอย่าง จงหา ห.ร.ม.ของ 12 , 18                          ตัวประกอบของ 12 คือ 1 , 2 , 3 , 4 ,6 , 12                          ตัวประกอบของ 18 คือ 1 , 2 , 3 , 6 , 9 ,18                          ตัวประกอบร่วมของ 12 และ 18 คือ 1 , 2 , 3 , 6                          ดังนั้น ห.ร.ม. ของ 12 และ 18 คือ 6                 วิธีที่ 2 วิธีแยกตัวประกอบ มีขั้นตอนดังนี้                 1) แยกตัวประกอบของจำนวนนับที่กำหนดให้                    2) พิจารณาผลในข้อ 1 ว่ามีจำนวนใดซ้ำกันทุกบรรทัดบ้าง                   3) นำจำนวนที่ซ้ำกันในข้อ 1 คูณกัน                      4) ผลคูณที่ได้จากข้อ 3 เป็น ห.ร.ม.                           ตัวอย่าง จงหา ห.ร.ม.ของ 12 , 18                        12 = 2 x 2 x 3                        18 = 2 x 3 x 3                        ดังนั้น ห.ร.ม. ของ 12 และ 18 คือ 2 x 3 = 6                 วิธีที่ 3 วิธีตั้งหาร มีขั้นตอนดังนี้                  1) หารจำนวนนับที่กำหนดให้ด้วยตัวประกอบเเฉพาะของมัน                  2) หารผลหารที่ได้จากข้อ 1 ด้วยตัวประกอบเฉพาะ                  3) ในกรณีที่ไม่มีตัวประกอบเฉพาะใดหารผลหารได้ลงตัวทั้งหมด จะหยุดทำการหารทันที                  4) นำตัวหารทั้งหมดคูณกัน ผลคูณที่ได้คือ ห.ร.ม.                  ตัวอย่าง จงหา ห.ร.ม.ของ 12 , 18                                  2 ) 12 , 18                                    3 )  6 ,  9                                         2 , 3                   ดังนั้น ห.ร.ม. ของ 12 และ 18 คือ 2 x 3 = 6                 วิธีที่ 4 วิธียูคลิก เป็นวิธีการหา ห.ร.ม. ที่เหมาะในกรณีที่มีจำนวนนับ 2 จำนวน และจำนวนนับนั้นมีค่ามาก ๆ ซึ่งมีขั้นตอนดังนี้                  1) นำจำนวนนับที่มีค่าน้อยไปหารจำนวนนับที่มีค่ามาก                  2) จากข้อ 1 ถ้ามีเศษ ให้นำเศษไปหารำนวนนับที่เป็นตัวหารในข้อ 1                  3) ปฎิบัติเช่นนี้ไปเรื่อย ๆ จนกระทั่งพบว่าจำนวนนับใดที่เหลือจากการหารแล้วหารลงตัว จำนวนนั้นแหละคือ ห.ร.ม. ค.ร.น

ค.ร.น. บางทีเรียกว่า คูณร่วมน้อย หมายถึง ตัวคูณร่วมที่มีค่าน้อยที่สุด                 ค.ร.น.. จะเกิดขึ้นเมื่อมีจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป                 การหาร ค.ร.น.สามารถหาได้หลายวิธี ดังนี้                 วิธีที่ 1 วิธีหาตัวประกอบ มีขั้นตอนดังนี้                 1) หาว่าจำนวนนับที่กำหนดมาให้เป็นตัวประกอบของจำนวนใดบ้าง                 2) หาตัวคูณร่วมของข้อ 1                 3) นำตัวคูณร่วมที่มีค่าน้อยที่สุดในข้อ 2 เป็น ค.ร.น.                  ตัวอย่าง จงหา ค.ร.น. ของ 12 , 18                          12 เป็นตัวประกอบของ 12 , 24 , 36 , 48 , 60 , 72 , ...                          18 เป็นตัวประกอบของ 18 , 36 , 54 , 72 , 90 , ...                          ตัวคูณร่วมของ 12 และ 18 คือ 36 ,72 , ...                          ดังนั้น ค.ร.น.. ของ 12 และ 18 คือ 36                 วิธีที่ 2 วิธีแยกตัวประกอบ มีขั้นตอนดังนี้                 1) แยกตัวประกอบของจำนวนนับที่กำหนดให้                   2) พิจารณาผลในข้อ 1 ว่ามีจำนวนใดซ้ำกันทุกบรรทัดบ้าง ในกรณีที่ไม่มีจำนวนซ้ำกันทุกบรรทัด สามารถลดหลั่นลงได้                  3) นำจำนวนที่ได้ในข้อ 2 คูณกัน                  4) ผลคูณที่ได้จากข้อ 3 เป็น ค.ร.น.                           ตัวอย่าง จงหา ห.ร.ม.ของ 12 , 18                        12 = 2 x 2 x 3                        18 = 2 x 3 x 3                        ดังนั้น ห.ร.ม. ของ 12 และ 18 คือ 2 x 3 x 2 x 3 = 36                        หรือ ห.ร.ม. ของ 12 และ 18 คือ x                 วิธีที่ 3 วิธีตั้งหาร มีขั้นตอนดังนี้                  1) หารจำนวนนับที่กำหนดให้ด้วยตัวประกอบเเฉพาะของมัน                  2) ในกรณีที่หารไม่ลงตัวทั้งหมด สามารถลดหลั่นได้ตามลำดับ                  3) หารไปเรื่อย ๆ จนผลหารของทุกจำนวนมีค่าเท่ากับ 1                  4) นำตัวหารทั้งหมดคูณกัน ผลคูณที่ได้คือ ค.ร.น.                  ตัวอย่าง จงหา ห.ร.ม.ของ 12 , 18                                  2 ) 12 , 18                                    3 )  6 ,  9                                      2 )2 , 3                                       3 )1 , 3                                             1 , 1                   ดังนั้น ห.ร.ม. ของ 12 และ 18 คือ 2 x 3 x 2 x 3 = 36

 อ้างอิง http://home.kku.ac.th/chulao/math/content/factor/factor_content.htm 30/08/2556